Hace tiempo que quería preparar un tema así, dado que existe mucha información por internet pero creo que necesitábamos tenerlo en el foro. Se habla por ejemplo en otros hilos de números capicua en los euros. Dada la naturaleza de estos números de serie se trata de algo sumamente raro.
Los números de serie de los euros están normalmente compuestos por una letra seguida de once números.
La letra representa al país emisor (en la serie Europa son dos letras), según una tabla como esta:
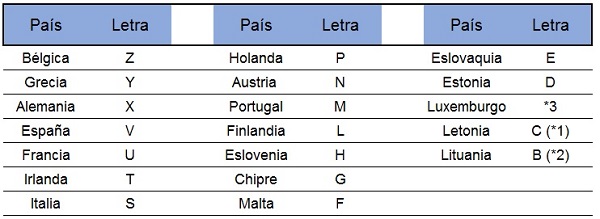
Del resto de cifras, la última es la cifra de comprobación o
checksum. Este número jamás puede ser 0.
Para calcularlo se sustituye el valor de la letra del país emisor siguiendo esta tabla:

A continuación se divide el número resultante entre 9 y se examina el resto que debe ser siempre 8. Esto puede realizarse fácilmente sumando cada cifra de manera individual y luego sumando las cifras del resultado y así hasta reducirlo a un número inferior a 9.
Tomando un ejemplo de un billete español (V=22), el checksum se puede calcular con una ecuación simple (checksum = x):
221618626962x (la suma dígito a dígito ha de ser igual a

2+2+1+6+1+8+6+2+6+9+6+2+x = 8
51 + x = 8
5+1+x = 8
6 + x = 8
x = 8 - 6
x = 2 (el checksum de ese billete es 2)
También existe la
suma de verificación. Para este cálculo se emplean sólo las 11 cifras, que tras operar con sus números por el mismo método (división entre 9 y ver el resto), debe resultar en la cifra asignada para ese país, según esta tabla:

Eso quiere decir que un determinado número de serie no existe en todos los países. Y también que no pueden existir dos números correlativos de billete porque el checksum cambiaría automáticamente para compensar (si se incrementa en uno la cifra penúltima, el checksum disminuye en una unidad).
Visto y resumido de
http://elmurodelcoleccionista.com/viewtopic.php?t=53Así pues, ¿cuántos capicúas puede haber entre los euros? En teoría 900000 capicúas por letra pero la mayoría no serán viables. ¿Por qué? Porque el checksum final cambia según el resto. Y como cambia el checksum deberá cambiar también la primera cifra para que pueda ser capicúa. Por cada cifra que cambia el checksum será diferente por lo que no es posible que existan 9 x 10 x 10 x 10 x 10 x 10 capicúas.
Pongamos la matemática:
a b c d e f e d c b a
'a' sólo puede ser 9 cifras porque el 0 está prohibido en el checksum
el resto pueden ser de 0 a 9
Por ello el total potencial podría ser 9 x 10 x 10 x 10 x 10 x 10 = 900000
A modo de ejemplo, el número de serie V11111111111 no sería un número válido porque la suma de verificación daría 2 y su checksum suma 6 y no 8.
Uno pensaría que basta con cambiar la cifra central por 3 (nótese que el 2 quedaría descartado automáticamente porque la suma no sería válida): V11111311111. La suma de verificación da 4 (correcto para España) pero el checksum da 3, por lo que no tampoco es una combinación válida.
De esta manera ningún serial 11111x11111 sería un número válido y por lo tanto descartaríamos 10 capicúas.
El primer capicúa que podría ser válido sin ceros sería el V11112121111 (suma 4 y checksum

.
¿Y los que contengan ceros (la primera cifra sólo podrá ser >1)?
V10000000001 ==> suma = 2, checksum = 6. Habría que añadir 2 unidades
Así pues:
V10000200001 ==> suma = 4, checksum = 8.
V10001010001 ==> suma = 4, checksum = 8.
También serían seriales válidos capicúas:
V10010001001
V10100000101
V11000000011
Y a partir de aquí cualquier reparto de 9 puntos de manera simétrica:
V10001910001
V10010901001
V10100900101
V11000900011
Pero sobre la serie V10000200001 no se pueden añadir 9 puntos simétricamente salvo que se modifique la cifra central y se le sume una cifra impar (1, 3, 5, 7) porque de lo contrario no se pueden repartir los restos a ambos lados.
V10004340001
V10003530001
V10002720001
V10001910001
Esto restringe aún más las posibilidades. Evidentemente podemos posicionar esos 4, 3, 2, 1 en la segunda, tercera y cuarta cifra obteniendo 12 capicúas más, pero no podríamos alterar las cifrás más que sumando impares en la central y repartiendo.
No soy capaz de hacer la matemática para calcular cuántos capicúas son válidos para un billete español (V) pero como veis son muchos menos.
A modo de ejemplo, usando sólo 0 y 1, las combinaciones de capicúas de 11 cifras son 64, pero números de serie válidos son apenas 4, por lo que 60 no existirán nunca.
Usando 0, 1 y 2, los capicúas potenciales sería 729. Válidos serían muchísimos menos, aunque no he echado la cuenta, pero seguramente del orden de 20-30.
En teoría el sólido V22222222222 sí debería existir. De hecho es el único número sólido válido. Los demás (1, 3, 4, 5, 6, 7, 8, 9 y por supuesto 0) simplemente nunca aparecerán en un billete.
Con un 3 el primero válido sería V11111311111.
Espero que a pesar de lo desorganizado os haya interesado. A ver si me pongo a calcular bien y os doy datos más curiosos.
